小声bb:这东西就是个小抄,用来记不住式子的时候查一下子
公式整理
chap2
禁带宽度,T
对大多数IV,III-V,II-VI族,化合物半导体
E_g(T)=E_g(0K)-\frac{\alpha T^2}{\beta+T}有效质量
m^*=\frac{\hbar^2}{(\frac{d^2E}{dk^2})}chap4
平衡载流子密度
n_0=N_C\cdot e^{-\frac{E_C-E_F}{k_0 T}},p_0=N_V\cdot e^{-\frac{E_F-E_V}{k_0 T}}其中
N_C=2(\frac{2\pi m_n^*k_0T}{h^2})^{3/2}\propto T^{3/2},N_V=2(\frac{2\pi m_p^*k_0T}{h^2})^{3/2}\propto T^{3/2}若E_{Fi}\approx E_i=\frac{E_C+E_V}{2}
n_0=n_ie^{\frac{E_F-E_i}{k_0T}},p_0=n_ie^{\frac{E_i-E_F}{k_0T}}质量作用定律
对平衡载流子
n_0\cdot p_0=n_i^2简并非简并的概念
当浓度较小时,为非简并,服从玻尔兹曼分布
当浓度较大时,进入非简并状态,此时平衡载流子浓度大于$N_C$或$N_V$
本征半导体载流子
n_i=n_{0i}\cdot p_{0i}=\sqrt{N_CN_V}e^{-\frac{E_g}{2k_0T}}非本征半导体的载流子
对施主能级上的电子浓度
n_D=N_Df_D(E)=\frac{N_D}{1+\frac{1}{g_D(E)}e^{\frac{E_D-E_F}{k_0T}}}电离施主浓度
n_D^+=N_D(1-f_D(E))=\frac{N_D}{1+g_D(E)e^{-\frac{E_D-E_F}{k_0T}}}g_D(E)=2对受主能级上的空穴浓度
n_A=N_Af_A(E)=\frac{N_A}{1+\frac{1}{g_A(E)}e^{\frac{E_F-E_A}{k_0T}}}电离空穴浓度
n_A^-=N_A(1-f_A(E))=\frac{N_A}{1+g_A(E)e^{-\frac{E_F-E_A}{k_0T}}}g_A(E)=4电中性关系
p_0+\sum_{i=1}^nn_{Di}^+=n_0+\sum_{j=1}^mp_{Aj}^-非平衡载流子(对n-type)
对载流子的注入和抽取,分别有
np>n_i^2;np< n_i^2小注入条件
n-type
p_0<(\Delta p=\Delta n)< n_0p-type
n_0<(\Delta p=\Delta n)< p_0-
非平衡载流子寿命
- 符号定义
N_t复合中心浓度,n_t复合中心的电子浓度,G_n,G_p过剩电子发射率和过剩电子的发射率,R_n,R_p过剩电子俘获率和过剩空穴俘获率,\tau_n,\tau_p过剩少子寿命.\Delta p(t)=(\Delta p)_0e^{-\frac{t}{\tau}}对复合下
\tau=\frac{1}{U_d}\Delta p- 直接复合
r为电子-空穴复合几率U_d=R-G_0=rnp-rn_i^2=r(n_0+p_0)\Delta p+r(\Delta p)^2\tau=\frac{1}{r(n_0+p_0)+r\Delta p} - 间接复合
r_n,r_p为复合中心俘获电子和空穴能力的强弱
g_n,g_p为复合中心发射电子和空穴的能力强弱
净复合率(SRH复合理论)U=\frac{N_tr_nr_p(np-n_i^2)}{r_n(n+n_l)+r_p(p+p_l)}带入强n,p型的条件,可得
U=\frac{np-n_i^2}{\tau_p(n+n_l)+\tau_n(p+p_l)}载流子寿命
\tau=\frac{\Delta p}{U}=\Delta p\cdot\frac{\tau_p(n+n_l)+\tau_n(p+p_l)}{np-n_i^2}低复合中心浓度时(
\tau_p=\tau_n)U=\frac{N_tr(np-n_i^2)}{n+p+2n_i\ch(\frac{E_t-E_i}{k_0T})}
陷阱
陷阱的电子浓度为
\Delta n_t=\frac{N_tn_l}{(n_0+n_l)^2}\cdot\Delta n最有效的陷阱是少子陷阱,陷阱能级越靠近费米能级越有效
准费米能级
对非平衡态有
n=N_Ce^{-\frac{E_C-E_F^n}{k_0T}},p=N_Ve^{-\frac{E_F^p-E_V}{k_0T}}E_F^n,E_F^p为准费米能级
chap5
漂移电流密度
J_{dp}=pqv_{dp}=pq\mu_pEJ_{dn}=nqv_{dn}=nq\mu_nE迁移率
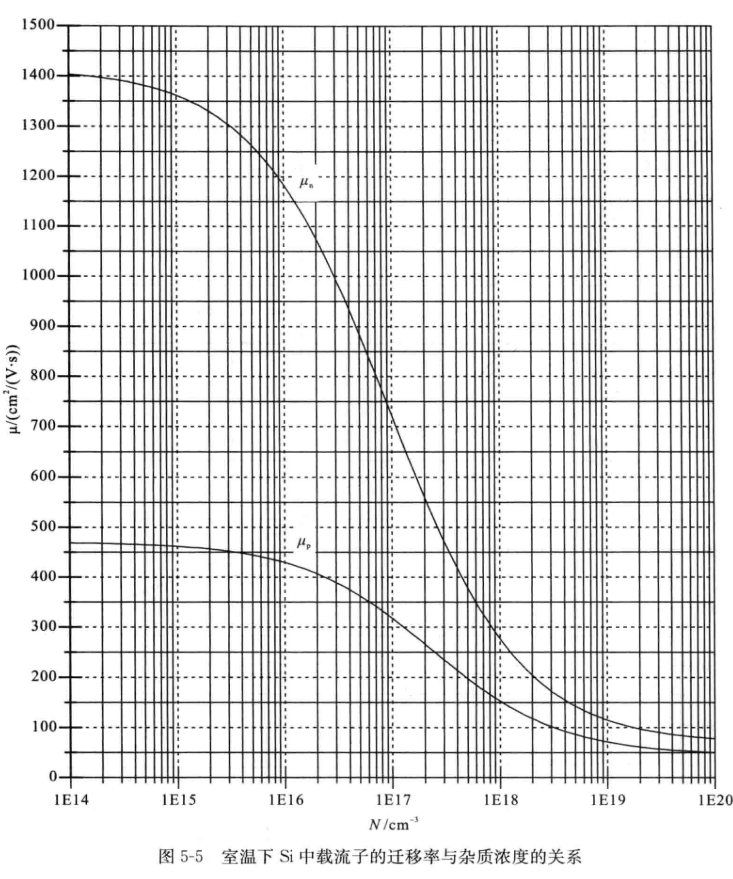
\mu_n=\frac{v_{dn}}{E}=\frac{q\tau_n}{m_n^*}\mu_p=\frac{v_{dp}}{E}=\frac{q\tau_p}{m_p^*}迁移率浓度图像
散射
平均自由时间\tau
- 电离杂质散射
\tau_i\propto\frac{T^{3/2}}{N_i},N_i=N_A+N_D散射概率
P=\frac{1}{\tau}只有电离杂志散射的迁移率
\mu_i\propto\frac{T^{3/2}}{N_i} -
晶格振动散射
只有声学波声子散射存在时\tau_s\propto T^{-3/2},\mu_s\propto T^{-3/2}光学波声子散射,
v为光学波声子频率\tau_o\propto\frac{(e^{\frac{hv}{k_0T}}-1)f(\frac{hv}{k_0T})}{T^{1/2}},\mu_o\propto(e^{\frac{hv}{k_0T}}-1)
总迁移率
\frac{1}{\mu}=\frac{1}{\mu_i}+\frac{1}{\mu_s}+\frac{1}{\mu_o}近似公式
\mu=\frac{q}{m_n^*}\cdot(\frac{aN_i}{T^{3/2}}+bT^{3/2})^{-1}前半段控制低温部分,后半段控制高温部分
电导率
J_{dp}=\sigma_pE\Rightarrow\sigma_p=pq\mu_pJ_{dn}=\sigma_nE\Rightarrow\sigma_n=nq\mu_n总电导率
\sigma=\sigma_n+\sigma_p=nq\mu_n+pq\mu_p扩散运动
L_p=\sqrt{D_p\tau},D_p为空穴扩散系数,L_p为空穴扩散长度
一般解
\Delta p(x)=Ae^{-x/L_p}+Be^{x/Lp}样品很厚时
\Delta p(x)=(\Delta p)_0\cdot e^{-x/L_p}样品厚度为W,足够薄时,为线性衰减
\Delta p(x)\approx(\Delta p)_0(1-x/W)扩散电流
F_n,F_p为扩散流密度,F_n=-D_n\frac{dn}{dx},F_p=-D_p\frac{dp}{dx}
J_{n扩}=(-q)F_n=qD_n\frac{dn}{dx}J_{p扩}=(+q)F_p=-qD_p\frac{dp}{dx}电流密度方程
总电流密度为
J_n=J_{n漂}+J_{n扩}=nq\mu_nE+qD_n\frac{dn}{dx}J_p=J_{p漂}+J_{p扩}=pq\mu_pE-qD_p\frac{dp}{dx}J=J_p+J_n爱因斯坦关系
利用平衡的半导体内部为电中性,净电流为0可以得到
\frac{D_n}{\mu_n}=\frac{k_0T}{q}\frac{D_p}{\mu_p}=\frac{k_0T}{q}连续性方程
\frac{\partial n}{\partial t}=D_n\frac{\partial^2n}{\partial x^2}+\mu_n|E|\frac{\partial n}{\partial x}+\mu_n n\frac{\partial|E|}{x}-\frac{\Delta n}{\tau_n}+g_n\frac{\partial p}{\partial t}=D_p\frac{\partial^2p}{\partial x^2}+\mu_p|E|\frac{\partial p}{\partial x}+\mu_p p\frac{\partial|E|}{x}-\frac{\Delta p}{\tau_p}+g_p