chap1-3

Chap1 矢量分析

直角坐标

grad\space u=\nabla u=(\frac{\partial u}{\partial x},\frac{\partial u}{\partial y},\frac{\partial u}{\partial z})

div\space \vec{F}=\nabla\cdot\vec{F}=\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}+\frac{\partial F_z}{\partial z}

rot\space\vec{F}=\nabla\times\vec{F}=
\begin{vmatrix}
e_x&e_y&e_z\\
\frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\
F_x&F_y&F_z
\end{vmatrix}

柱坐标

grad\space u=\nabla u=(\frac{\partial u}{\partial \rho},\frac{\partial u}{\rho\partial\phi},\frac{\partial u}{\partial z})

div\space \vec{F}=\nabla\cdot\vec{F}=\frac{1}{\rho}\frac{\partial}{\partial\rho}(\rho F_\rho)+\frac{1}{\rho}\frac{\partial}{\partial\phi}(F_\phi)+\frac{\partial F_z}{\partial z}

rot\space\vec{F}=\nabla\times\vec{F}=\frac{1}{\rho}
\begin{vmatrix}
e_\rho&\rho e_\phi&e_z\\
\frac{\partial}{\partial \rho}&\frac{\partial}{\partial \phi}&\frac{\partial}{\partial z}\\
F_\rho&\rho F_\phi&F_z
\end{vmatrix}

球坐标

grad\space u=\nabla u=(\frac{\partial u}{\partial r},\frac{\partial u}{r\partial\theta},\frac{\partial u}{r\sin\theta\partial \phi})

div \space\vec{F}=\nabla\cdot\vec{F}=\frac{1}{r^2}\frac{\partial}{\partial r}(r^2F_r)+\frac{1}{r\sin\theta}\frac{\partial}{\partial\theta}(\sin\theta F_\theta)+\frac{1}{r\sin\theta}\frac{\partial}{\partial\phi}(F_\phi)

rot\space\vec{F}=\nabla\times\vec{F}=\frac{1}{r^2\sin\theta}
\begin{vmatrix}
e_r&r e_\theta&r\sin\theta e_\phi\\
\frac{\partial}{\partial \rho}&\frac{\partial}{\partial \phi}&\frac{\partial}{\partial z}\\
F_r&r F_\theta&r\sin\theta F_\phi
\end{vmatrix}

高斯定理

\int_V\nabla\cdot\vec{F}dV=\oint_S\vec{F}\cdot d\vec{S}

空间内的散度的体积分相当于包围空间的闭合曲面的通量

斯托克斯公式

\int_S\nabla\times\vec{F}dS=\oint_C\vec{F}\cdot d\vec{l}

平面内旋度的面积分相当于平面边界的环流

梯度场无旋

\nabla\times(\nabla u)\equiv0

旋度场无散

\nabla\cdot(\nabla\times\vec{F})\equiv0

Chap2 电磁场基本规律

电荷守恒定律

\oint_S\vec{J}\cdot d\vec{S}=-\frac{d}{dt}\int_V\rho dV

\nabla\cdot\vec{J}+\frac{\partial \rho}{\partial t}\equiv0

真空电场方程

F_{12}=\vec{e_R}\frac{q_1 q_2(\vec{r_1}-\vec{r_2})}{4\pi\varepsilon_0|\vec{r_2}-\vec{r_1}|^3}=\frac{q_1q_2}{4\pi\varepsilon_0R^3}\vec{R}

真空磁场

F_{12}=\frac{\mu_0}{4\pi}\oint_{C_1}\oint_{C_2}\frac{I_2d\vec{l_2}\times[I_1d\vec{l_1}\times(\vec{r_2}-\vec{r_1})]}{|\vec{r_2}-\vec{r_1}|^3}

Maxwell

积分形式

\begin{matrix}
\oint_C\vec{H}\cdot d\vec{I}=\int_S(\vec{J}+\frac{\partial \vec{D}}{\partial t})\cdot d\vec{S}\\ \\
\oint_C\vec{E}\cdot d\vec{l}=-\int_S\frac{\partial B}{\partial t}\cdot d\vec{S}\\ \\
\oint_S\vec{B}\cdot d\vec{S}=0\\\\
\oint_S\vec{D}\cdot d\vec{S}=q
\end{matrix}

微分形式

\begin{matrix}
\nabla\times\vec{H}=\vec{J}+\frac{\partial\vec{D}}{\partial t}\\\\
\nabla\times\vec{E}=-\frac{\partial\vec{B}}{\partial t}\\\\
\nabla\cdot\vec{B}=0\\\\
\nabla\cdot\vec{D}=\rho
\end{matrix}

媒质电磁特性

\begin{matrix}
\vec{D}=\varepsilon\vec{E}\\\\
\vec{B}=\mu\vec{H}\\\\
\vec{J}=\sigma\vec{E}
\end{matrix}

磁化电流与极化电荷

\begin{matrix}
\rho_{se}=\vec{e_n}\cdot\vec{P},\rho_e=-\nabla\cdot\vec{P}\\\\
\vec{J}_m=\nabla\times\vec{M},\vec{J}_{sm}=\vec{e_n}\times(\vec{M_1}-\vec{M_2})
\end{matrix}

电磁场的边界条件

介质的定义

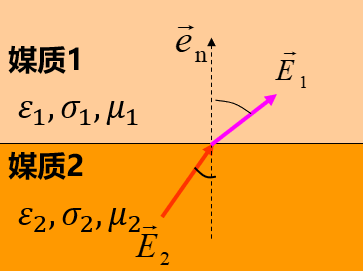
一般形式/导体表面

\begin{matrix}
\vec{e_n}\times(\vec{H_1}-\vec{H_2})=\vec{J_S}\\\\
\vec{e_n}\times(\vec{E_1}-\vec{E_2})=0\\\\
\vec{e_n}\cdot(\vec{B_1}-\vec{B_2})=0\\\\
\vec{e_n}\cdot(\vec{D_1}-\vec{D_2})=\rho_S\\\\
\end{matrix}

理想介质面

\begin{matrix}
\vec{e_n}\times(\vec{H_1}-\vec{H_2})=0&H_{1t}-H_{2t}=0\\\\
\vec{e_n}\times(\vec{E_1}-\vec{E_2})=0&E_{1t}-E_{2t}=0\\\\
\vec{e_n}\cdot(\vec{B_1}-\vec{B_2})=0&B_{1n}-B_{2n}=0\\\\
\vec{e_n}\cdot(\vec{D_1}-\vec{D_2})=0&D_{1n}-D_{2n}=0\\\\
\end{matrix}

场内媒质参数

极化电荷

\begin{matrix}
\vec{P}=\chi_e\varepsilon_0\vec{E}\\\\
\vec{D}=\varepsilon_0\vec{E}+\vec{P}\\\\
\rho_P=-\nabla\cdot\vec{P},\rho_{SP}=\vec{P}\cdot\vec{e_n}
\end{matrix}

磁化电流

\begin{matrix}
\vec{M}=\chi_m\vec{H}\\\\
\vec{B}=(1+\chi_m)\mu_0\vec{H}\\\\
(1+\chi_m)\mu_0=\mu\\\\
\vec{J_M}=\nabla\times\vec{M},\vec{J_{SM}}=\vec{M}\times\vec{e_n}
\end{matrix}

chap3 静态电磁场

电位函数

\vec{E}=-\nabla\phi,\phi=-\int{\vec{E}\cdot d\vec{l}}

电位函数在分界面的情况

导体分界面

\phi=const,\varepsilon\frac{\partial\phi}{\partial n}=-\rho_S

介质分界面

\rho_s=0\Rightarrow\varepsilon_2\frac{\partial\phi_2}{\partial n}=\varepsilon_1\frac{\partial\phi_1}{\partial n}

电容

C=\frac{q}{\phi}=\frac{q}{|\phi_1-\phi_2|}

静电场储能

w_e=\frac{1}{2}\vec{D}\cdot\vec{E}

恒定电场特性

空间中

\nabla^2\phi=-\frac{1}{\varepsilon}\rho

导体内:无自由电荷堆积

\sum_iI_i=0,\rho_f=0

边界

\vec{J_{1n}}=\vec{J_{2n}},\vec{D_{1n}}-\vec{D_{2n}}=\rho_S,\vec{E_{1t}}=\vec{E_{2t}}

恒定电场耗能

w=\vec{E}\cdot\vec{J}

矢量磁位

\vec{B}=\nabla\times\vec{A},\nabla^2\vec{A}=-\mu\vec{J}

恒定磁场边界条件

空间中

\nabla\times\vec{H}=\vec{J},\nabla\cdot\vec{B}=0

磁体内

\vec{B}=\mu\vec{H}

边界

\vec{B_{1n}}-\vec{B_{2n}}=0
\vec{H_{1t}}-\vec{H_{2t}}=\vec{J_S}

电感

1. 磁链:环路所包围的磁通量
   

   自感

   L=\frac{\Phi}{I}=L_i+L_o=\frac{\Phi_i}{I}+\frac{\Phi_o}{I}

   互感

   M=\frac{\Phi_{21}}{I}

   磁场储能

   w=\frac{1}{2}\vec{B}\cdot\vec{H}