半导体物理复习

Chap1晶体结构价键模型

半导体构型

• 元素半导体
  • 金刚石结构:C,Si,Ge
• 闪锌矿:III-V,II-VI族半导体
  

  Chap2半导体的电子结构

  直接带隙间接带隙

• 直接带隙:GaAs,GaN等
• 间接带隙:Si,C,Ge
  

  禁带宽度的温度变化

  E_g(T)=E_g(0K)-\frac{\alpha T^2}{\beta+T}

  对大多数III-V,IV,II-VI都比较有效

• 杂质浓度同样影响带宽,但是影响在1e18之前都比较小,可以忽略不记
  

  有效质量

  m^*=\frac{\hbar}{\frac{d^2E}{dk^2}}

  负的电子有效质量表示了运动等效正电荷的空穴
  对有效质量的意义

  f=m^*a=-qE

  越小的有效质量越高的加速度,等效质量为0的材料意味着有无穷大的加速度

  Chap3载流子定性描述

  载流子的复合与俘获

  复合

• 辐射复合:产生光子
• 无辐射复合:只产生声子

载流子寿命

\frac{1}{\tau}=\frac{1}{\tau_r}+\frac{1}{\tau_d}+\frac{1}{\tau_{Aug}}

分别表示直接复合寿命,间接复合寿命,俄歇复合寿命.
寿命的倒数为复合的几率

• 直接复合:Ec与Ev的电子空穴直接复合,根据半导体的能隙不同会产生声子或者只产生光子
• 间接复合:电子和空穴在复合中心或电子/空穴陷阱进行复合,所有的间接复合均不产生光子.
• 激子复合:激发态电子与价带空穴组成的双粒子体系,体系的复合就是激子复合
• 俄歇复合:三粒子过程,一对电子空穴复合,能量传递给第三个电子/空穴.无辐射,主要发生在重掺杂当中.
  

  Chap4载流子的定量统计描述

  n_0=N_c\cdot e^{-\frac{E_c-E_F}{k_0T}},p_0=N_v\cdot e^{-\frac{E_F-E_v}{k_0T}}

  n_0=n_i\cdot e^{-\frac{E_F-E_i}{k_0T}},p_0=p_i\cdot e^{-\frac{E_i-E_F}{k_0T}}

  n_0\cdot p_0=n_i^2=N_c\cdot N_ve^{-\frac{E_g}{k_0T}}

• 简并半导体:重掺杂下,Ec靠近EF,为重掺杂
  

  电中性关系

  p_0+\sum n_D^+=n_0+\sum p_A^-

  在这里,nD与pA指的是在杂质能级的电子和空穴
  

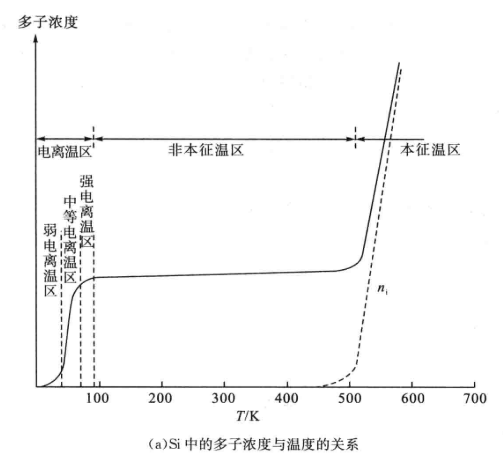
• 本征温度:达到本征温区时的临界温度
  

  Chap5三维半导体的载流子的电输运

  散射

  由于内部破坏周期性势场的因素而使载流子进入杂乱无章的状态.
  两次散射之间的运动才是有效的运动,考虑平均自由程.

• 电离杂质散射:由于杂质电离之后形成的带电粒子,形成库伦势场,产生散射.

  \tau_i \propto \frac{T^\frac{3}{2}}{N_i},N_i=N_A+N_D

• 晶格振动散射
  

  迁移率

  \mu_n=\frac{\tau_n q}{m_n^*},\mu_p=\frac{\tau_p q}{m_p^*}

  与平均自由时间成正比

  电导率

  J=\sigma E

  \sigma_n=nq\mu_n,\sigma_p=pq\mu_p

  扩散运动/扩散电流

  扩散运动

• 对足够厚的样品,以扩散长度指数衰减分布
• 对薄样片,线性衰减
  

  扩散电流

  J_{n}=qD_n\frac{dp}{dx},J_p=-qD_p\frac{dp}{dx}

  爱因斯坦关系

  核心是浓度梯度形成的内建电场与电流平衡

  \frac{D_n}{\mu_n}=\frac{k_0 T}{q},\frac{D_p}{\mu_p}=\frac{k_0 T}{q}

  Chap7 M-S接触

  几个定义

• 功函数:W_s=E_0-E_F
• 电子亲合能:\chi=E_0-E_c
• E_n=E_c-E_{Fs}
• W_s=\chi+E_n
  

  整流接触

• n型:W_m>W_s
• p型:W_s>W_m
  

  肖特基势垒(n型为例)

• 半导体到金属:qV_D=-qV_s=W_m-W_s
• 金属到半导体(肖特基势垒):q\phi_{ns}=E_g-(W_m-\chi)
  

  电流输运

  热电子发射理论

  核心:势垒区很薄,势垒边缘的电子能直接穿越,此时的势垒区宽度不重要,高度成为关键.利用s到m的运输进行分析,并在零偏压的情况下计算反向电流
  理查逊常数

  A^*=\frac{4\pi qm_n^*k_0^2}{h^3}

  反向饱和电流密度

  J_{ST}=A^*T^2\cdot exp(-\frac{q\phi_{ns}}{k_0T})

  I-V特性

  J_{s\to m}=J_{ST}\cdot exp(\frac{qV}{k_0T})W,J_{m\to s}=J_{ST}

  J=J_{ST}\cdot [exp(\frac{qV}{k_0T})-1]

  扩散理论

  核心:当迁移率较低的时候,势垒区宽度大于平均自由程,发生碰撞
  耗尽区宽度

  x_d=\sqrt{\frac{2\varepsilon_r\varepsilon_0(V_D-V)}{qN_D}}

  其他影响

• 镜像力:降低肖特基势垒,高电场反向电压下
• 隧道效应:反向偏压下,势垒降低
  

  势垒电容(交流电容)

  C=\frac{\varepsilon_0\varepsilon_r}{x_d},\frac{1}{C^2}=\frac{2}{\varepsilon_0\varepsilon_r qN_D}(V_D-V)

  斜率获得掺杂浓度,零点获得VD

  欧姆接触

• 极低的势垒高度,热电子直接发射
• 高的掺杂浓度,隧穿效应