背多分的镜像法

典例

点电荷对无限大接地导体平面

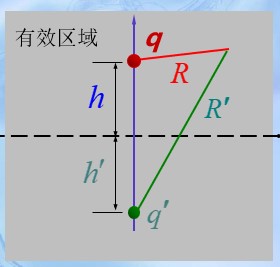
• 有效区域为z>0的区域

  \begin{matrix}
  q'=-q,h'=h\\\\\Phi=\frac{q}{4\pi\varepsilon}(\frac{1}{R}-\frac{1}{R'})
  \end{matrix}

  线电荷对无限大接地导体平面

  

• 有效区域为z>0

  \begin{matrix}
  \rho_l'=-\rho_l,h'=h\\\\
  \Phi=\frac{\rho_l}{2\pi\varepsilon}\ln\frac{R'}{R}
  \end{matrix}

  接地导体球面的镜像

  

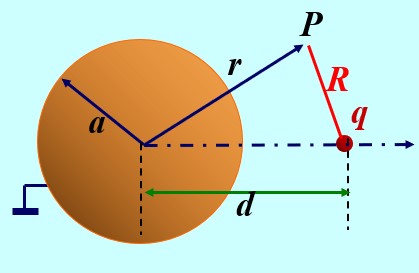
• 有效区域r>a

  \begin{matrix}
  d'=\frac{a^2}{d},q'=-\frac{a}{d}q\\\\
  \Phi=\frac{1}{4\pi\varepsilon}(\frac{q}{R}+\frac{q'}{R'})
  \end{matrix}

  不接地导体球面镜像

• 有效区域r>a,区别是多了一个位于O处的电荷,该电荷的作用使得球面的电势不为0,对该电荷

  q''=-q'=\frac{a}{d}q

  线电荷对导体圆柱面

  

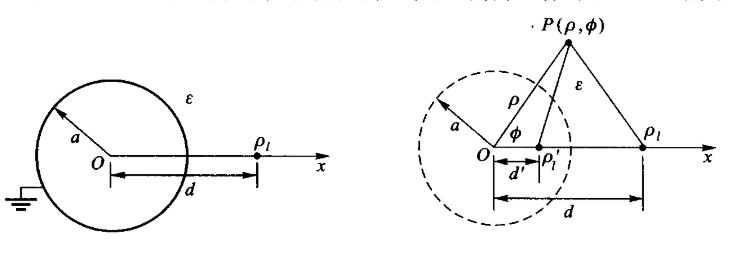
• 有效区域:r>a

  \begin{matrix}
  \rho_l'=-\rho_l,d'=\frac{a^2}{d}\\\\
  \Phi=\frac{\rho_l}{2\pi\varepsilon}\ln\frac{1}{R}+\frac{\rho_l'}{2\pi\varepsilon}\ln\frac{1}{R'}
  \end{matrix}

  两平行圆柱导体的电轴

  

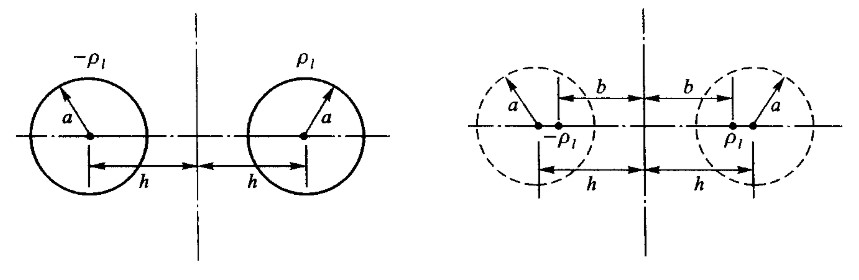
• 有效区域:圆柱导体外

  \begin{matrix}
  b=\sqrt{h^2-a^2},\rho_l=-\rho_l'\\\\
  \Phi=\frac{\rho_l}{2\pi\varepsilon}\ln\frac{R_-}{R_+}
  \end{matrix}

  介质平面成像

  
  

  

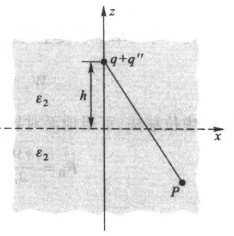
• 作用范围:无镜像电荷的一半空间

  \begin{matrix}
  q'=\frac{\varepsilon_1-\varepsilon_2}{\varepsilon_1+\varepsilon_2}q,q''=-\frac{\varepsilon_1-\varepsilon_2}{\varepsilon_1+\varepsilon_2}q
  \end{matrix}

  悟道:这里需要讲上下平面分开来看,对上部分进行分析的时候,将下半部分填充,此时的作用仅针对上半部分,对下半部分分析的时候,镜像和原电荷只针对上半部分

  悟道

  1. 镜像法的原理是唯一性定理,在求解区域内方程一定,边界条件一定的情况下解是唯一的.
  2. 镜像法使用的时候,首先需要划分求解域,并确定边界条件
  3. 确定了边界条件之后,将边界划分,对非求解域边界之外的部分可以进行任意的处理,使之满足常见的模型
  4. 进行成像,成像直到出现闭环为止.成像时必须保证所成的像不进入求解区域内
  5. 得到电位函数之后就可以很方便的获得电场分布能量等相关物理量了